(杂谈)卷积神经网络

2019-05-31 | 阅读：次

介绍

杂谈系列，主要来源各大网络资源库(知乎、CSDN、github等)牛人们的一些经典见解，我能只是知识的搬运工，同时发表一点自己的小看法，希望在搬运过程中有所收获。

为什么会分析卷积

CS231n给出了对卷积神经网络的解释：

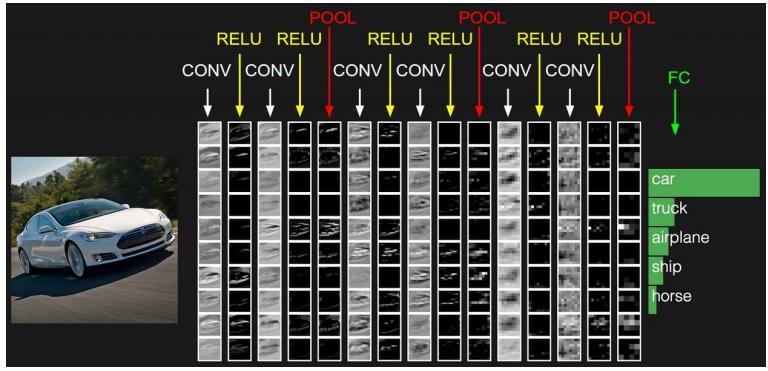
先说一下刚看到这张图的想法，当时觉得这是一种依赖于直觉的解释，也没有给出什么证明，所以自己对他们的解释也是相当的不满意，总感觉有种说不上来的困惑。前段时间用TensorFlow搭建卷积网络，又冒出了这个疑惑，便下决心找到一种能够让人心满意足的解释，于是便利用自己在信号处理课程上接触的卷积变换的相关知识，尝试着去理解卷积网络。想法已经产生，所以顺着想法尝试从底层思考，思路便渐渐清晰起来。以下便是我个人的一些微小的看法。

卷积神经网络（CNN）

先放一张比较经典的图片

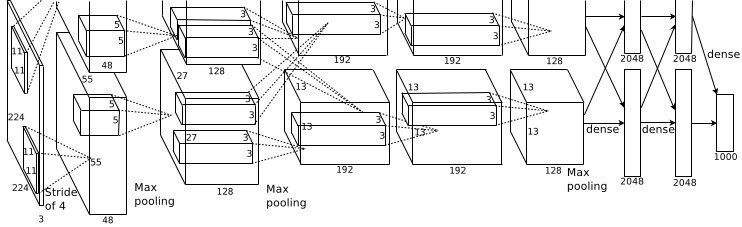
由于此文主要探讨卷积的作用，为了防止被自己带离节奏，这里不对该图做进一步解释，所以有感兴趣的可以参考AlexNet的讲解。

正文

> 卷积做了些什么

卷积这个名词，总容易使人感到不明觉厉，学数字信号处理的时候，就曾被这个名字搞得有点蒙圈，然而后来发现抛开名字，卷积做的事情并不复杂。

【注：深度学习中的卷积与信号处理中的卷积概念是有区别的，这里只介绍一下卷积神经网络中的卷积；所以以下所有卷积均指前者】

卷积操作可以被看做对输入的一种处理，大多数人正是因为把问题看得太复杂了，所以才感到有种被支配的感觉。其实卷积的操作就是加法和乘法的组合，与平时经常遇到的函数运算的区别是卷积操作具有时间或序列概念，是对数据的一个连续处理的过程，可以先通过一个一维结构数据的卷积来帮助理解。

假如有一段数据[1,1,1,0]

我们现在要对其做卷积操作

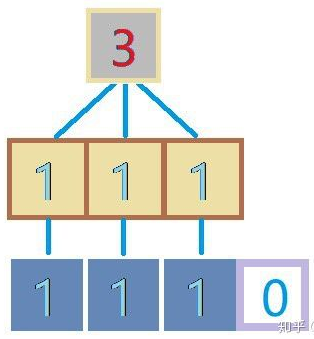
输入为[1;1;1;0]

中间一层我们称之为卷积核

而卷积操作过程其实很简单，也就是将卷积核与数据对应相乘，然后求和。所以对于上图，其操作过程便是1x1+1x1+1x1=3，“3”便是得到的结果或输出。但这只并不是卷积的整个过程，前面提到过，卷积操作是具有时间或序列属性的，而这只是整个卷积过程的其中一步，卷积复杂的地方也就在此，其实想想也没什么，剩下的都是些重复性操作，而整个卷积过程的输出便是这每一小小步产生结果的组合了。

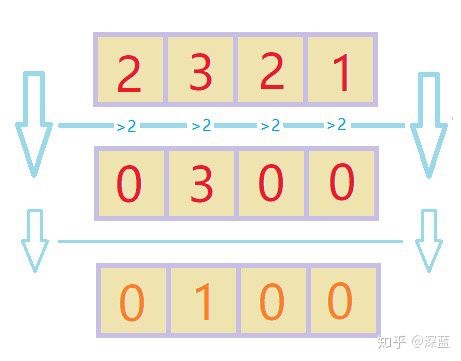
下面便是一个完整的卷积过程，为了让输入数据长度与输出数据相同；我们可以进行补零操作，也就是对边缘没有数据的地方按零处理（与卷积网络的Padding作用类似）。

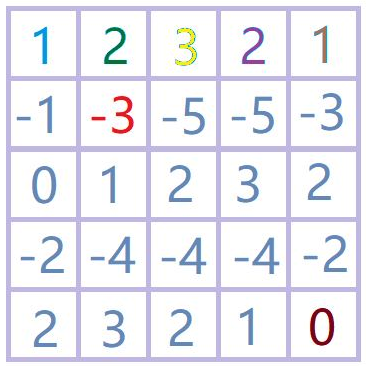
于是对于数据【1,1,1,0】在进行对边缘补一个零的操作后进行卷积的输出结果为

【2；3；2；1】（长度与输入相同）

而卷积的精髓其实是卷积核，换一个卷积核，卷积的输出结果便会迥然不同。

我们再来观察一下：

对于卷积核【1,-1,1】与【1,1,-1】

对数据【1,0,1,1,0】进行卷积处理的输出分别为：【-1,2,0,0,1】与【1,0,0,2,1】

由此可以发现，该例中卷积核的作用就是找到与它具有相同结构的数据，相似度越大，其对应输出也就相对越大（但这并不能作为一个结论去在实际中应用，因为实际卷积过程其实很复杂，而且是要涉及到反向传播的。比方说当卷积核有值取“0.5”时这句话就会失效，0.5x0.5的结果显然没有0.5x1的大，不过这也许能为卷积网络的设计提供一些想法上的参考。所以为了便于理解，本例卷积核仅取“+1”，“-1”，要处理的信息取值范围为[0,1]，而此处仅取“0”或“1”）；

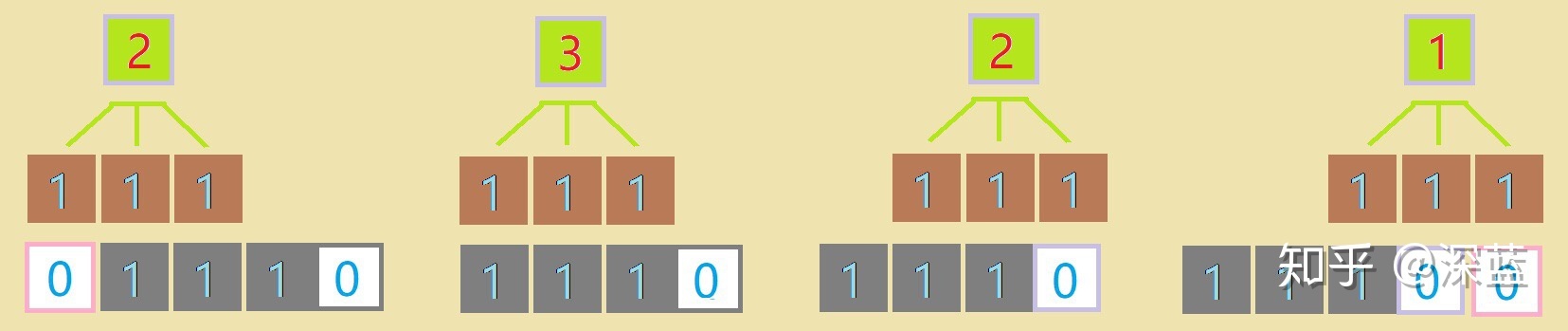
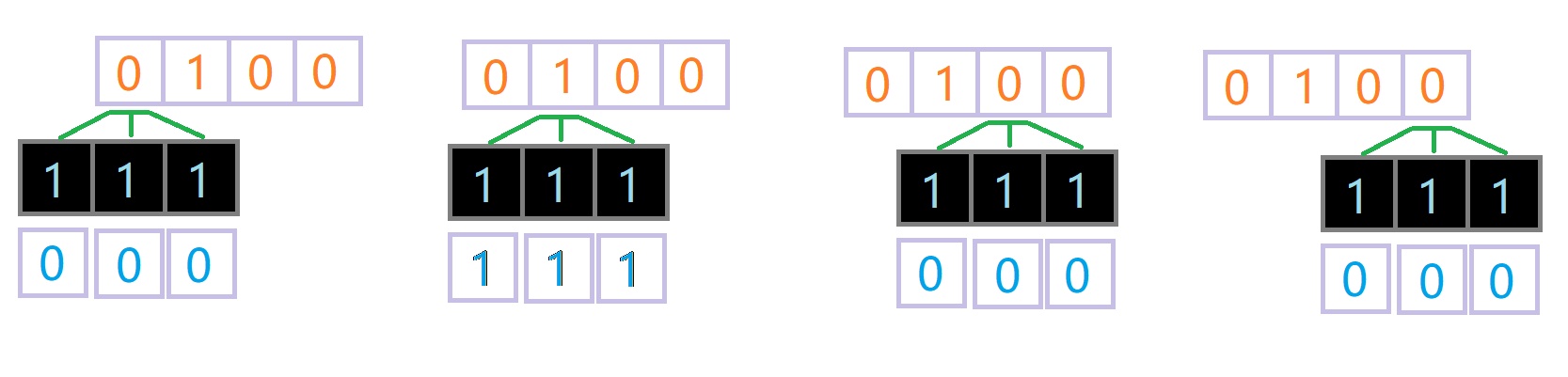
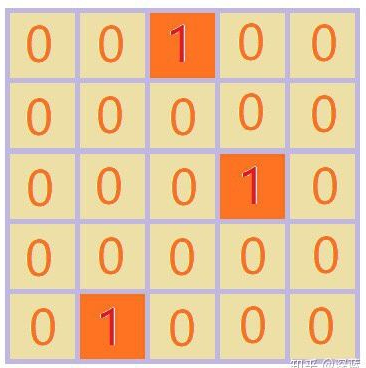
既然这个最大值是如此重要，我们完全可以忽略其余部分，把最重要的信息提取出来（这个过程有点类似于Sigmoid操作）；

下图为提取过程：

图中最底层对应为“1”的地方我们便可以理解为在它的上一层，包含有我们所检测的结构，这一信息；

也就是说，通过这一层中为“1”的位置可以反向找到与卷积核具有相同结构的数据。

过程见下图：

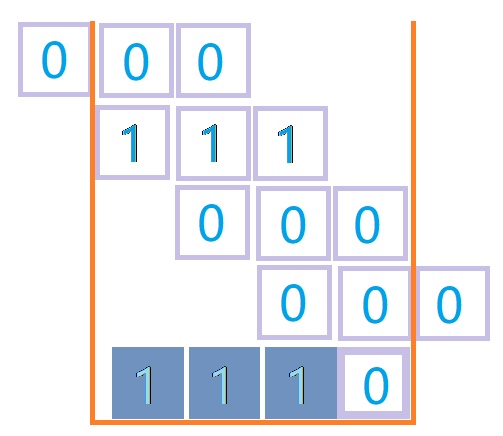
于是输入与输出就通过卷积操作对应了起来。

再举一个例子：

对二维结构的数据的卷积操作与一维数据的卷积类似，只不过卷积核也要相应的变为二维；

如：对于下面数据:

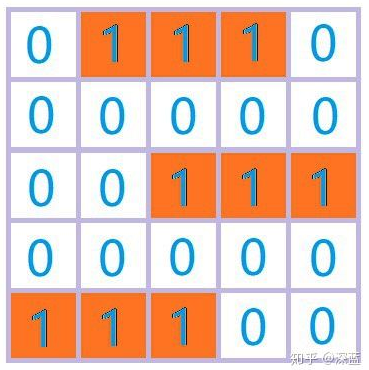
我们可以利用用下面这个卷积核:

对数据进行卷积操作:

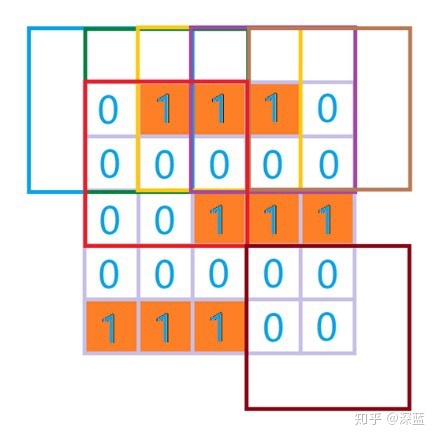
得到输出为:

(注意颜色之间的对应)

或许全局看更好一些:

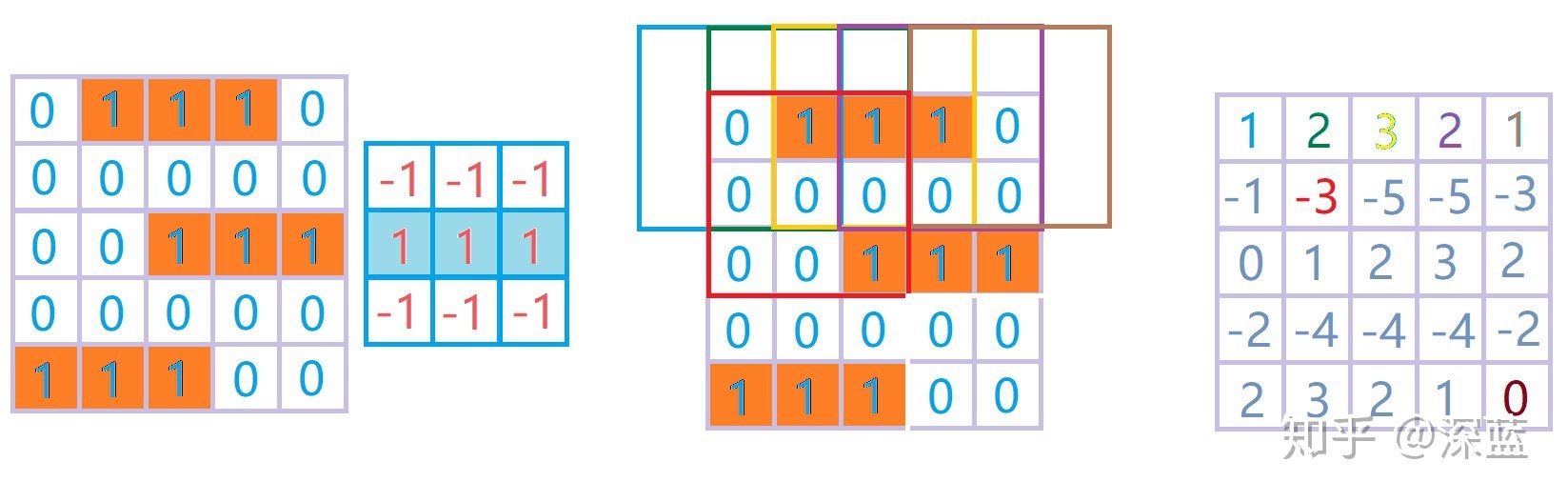
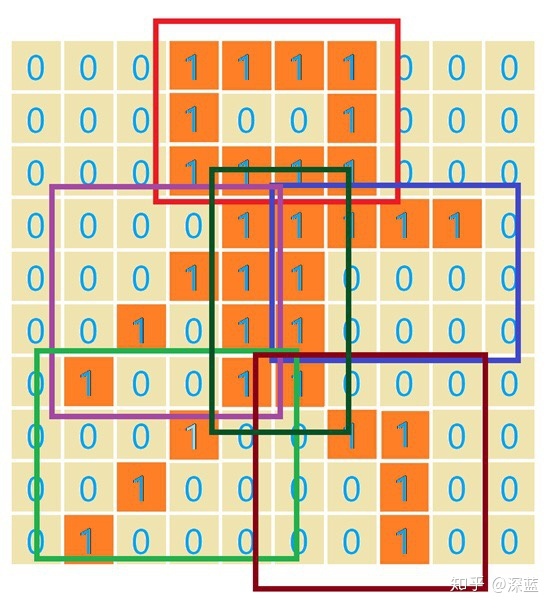
与一维数据的处理一样，我们同样可以提取出关键信息：

所以从图中可以看出，每一个“1”都与上层的橘黄色【1,1,1】所对应。

同样对于下面形状，

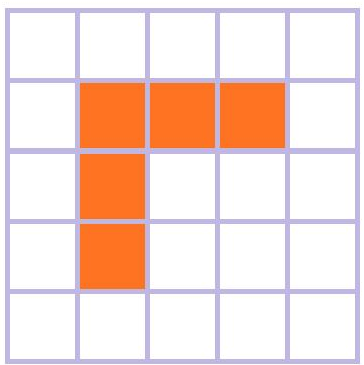
可以用下面卷积核来处理；

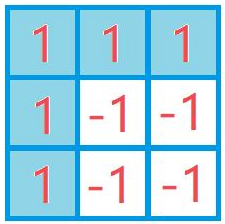
过程不在赘述。

> 二次卷积操作过程：

下面通过一个例子理解一下二次卷积操作：

对下面数据

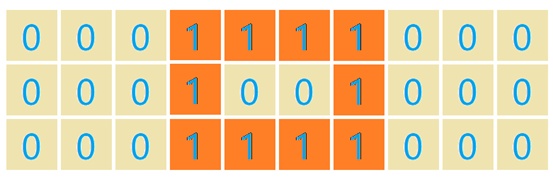
我们可以先用下面两个卷积核进行第一次处理；

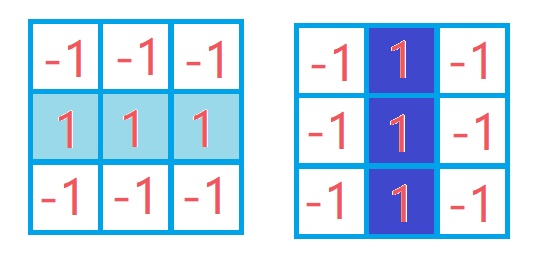
卷积输出经过关键信息提取后的结果为：

（注意颜色的相互对应）

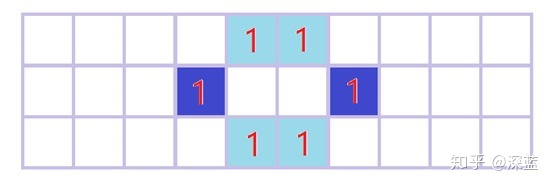
然后对上面的处理结果用下面卷积核进行第二次卷积操作；

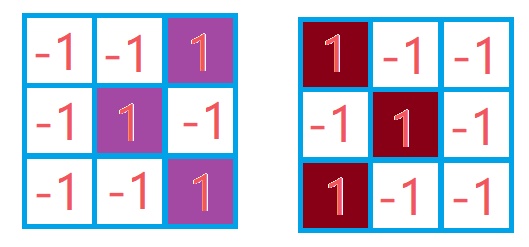
处理后的结果为（注意颜色）：

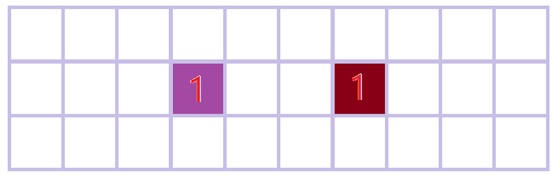
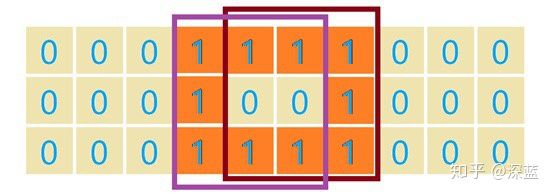
而上图每一个涂颜色框都与上上层数据的一个结构相关联；下面用不同颜色标了出来；

> 更深层次的探究：

有了这些理解我们就可以尝试一点更高级的玩意儿了，比方说识别一个“人”出来。

对你没听错，前提是我们的“人”长下面这样。

这里给出简要过程：

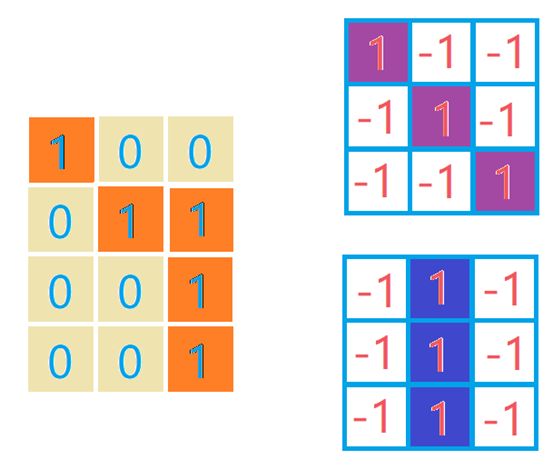
第一步：我们可以先通过下图右四个卷积核进行第一层卷积操作，并提取关键信息:

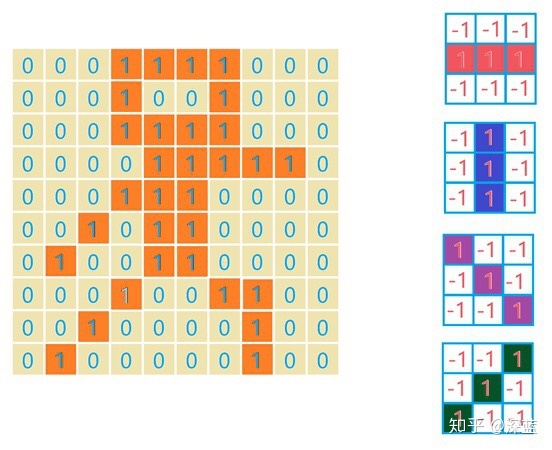
每一个卷积核对应的最后输出为：

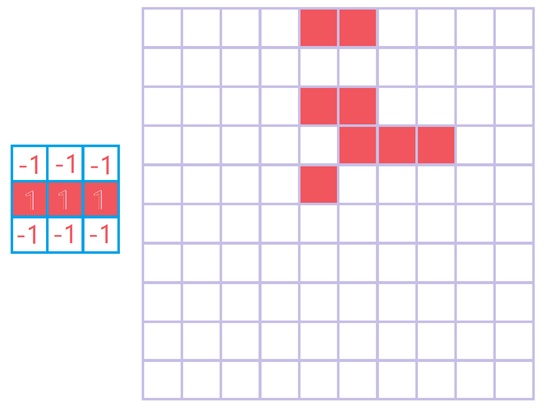
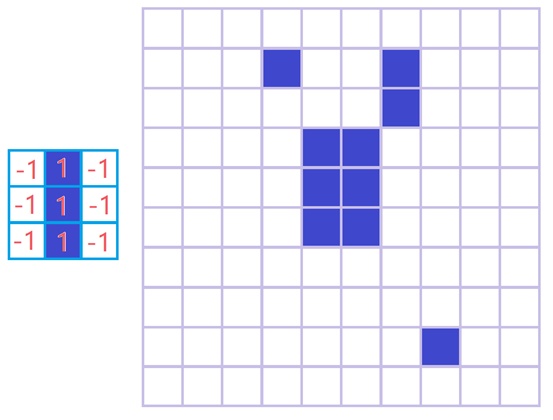
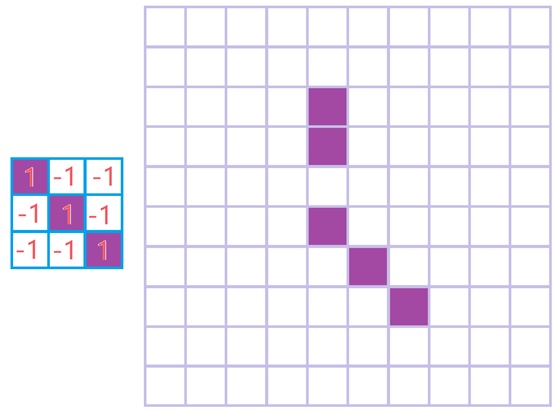
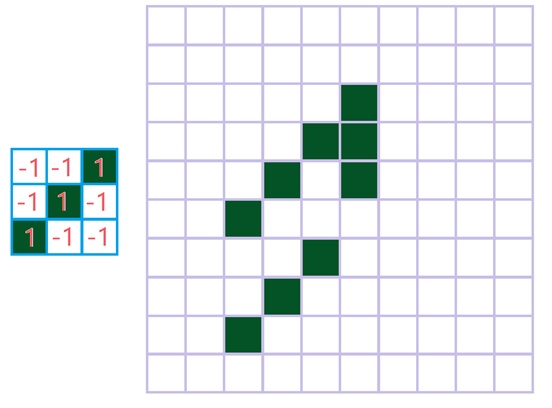
我们还可以将四层输出形成一个三维结构的数据（尝试思考一下三维卷积操作，是不是想出来了呢？对就是你想的那样）：

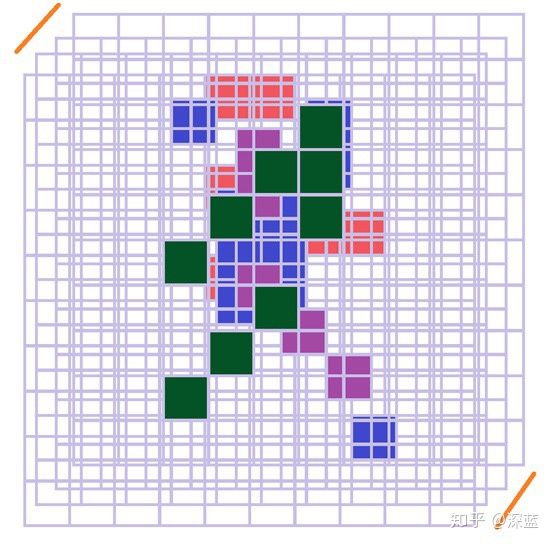
接下来我们就可以根据第一层卷积提取的结构，来提取更大的结构了；

如：头；前胳膊，后胳膊，左腿，右腿；还有身子；见下图

对于头：我们之前已经见识过了，当时利用的是下面两个卷积核对第一层输出进行的处理；

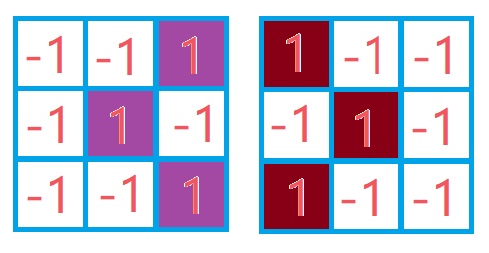
这里再举一个栗子加深理解：

下图左为这个人的右腿，经过第一层的卷积，其主要由下图右两部分组成，所以是否包含腿的信息可以经由下图右两部分结构的提取获得:

可以看出其实我们主要是从第一层卷积中的这两层（下图）提取出来蕴含“前腿”的信息的；

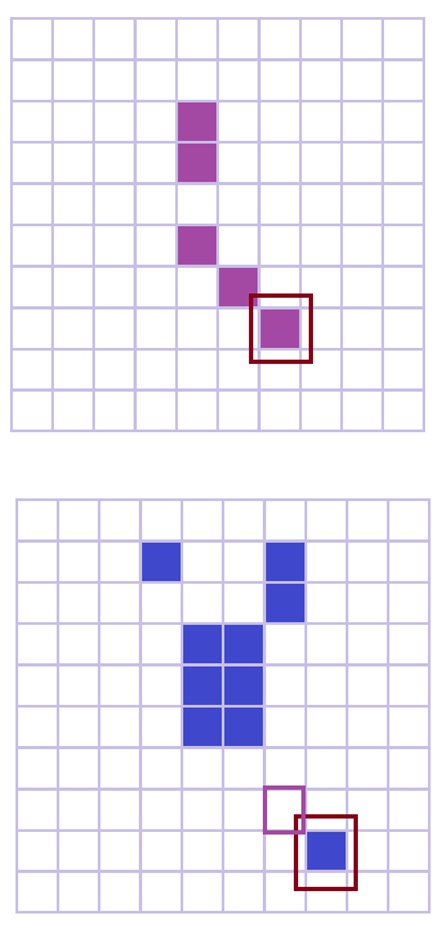
具体过程如下：

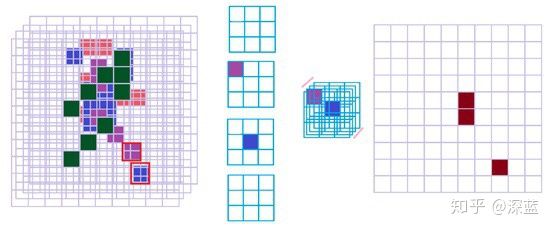
而卷积核的样子是这样的:

它是一个三维结构，共四层，每层都是3x3的结构；而它就是一个三维卷积操作的卷积核。

输出结果为：

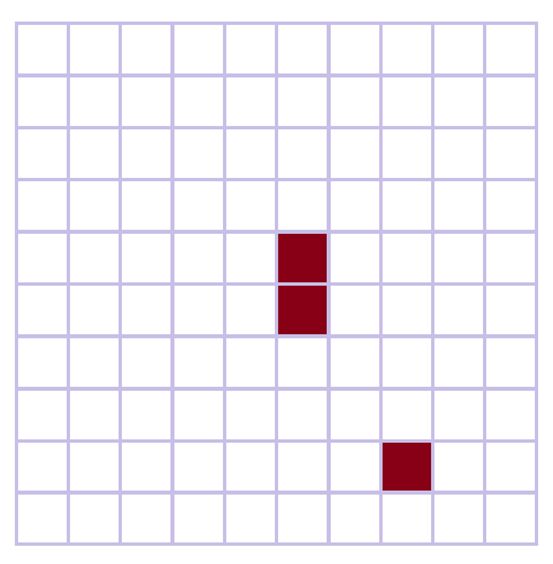
共有三条“腿”被检测了出来，从原始图中可以看出，只要是具有与我们要检测的“前腿”具有相同结构的地方都被我们检测了出来；见下图

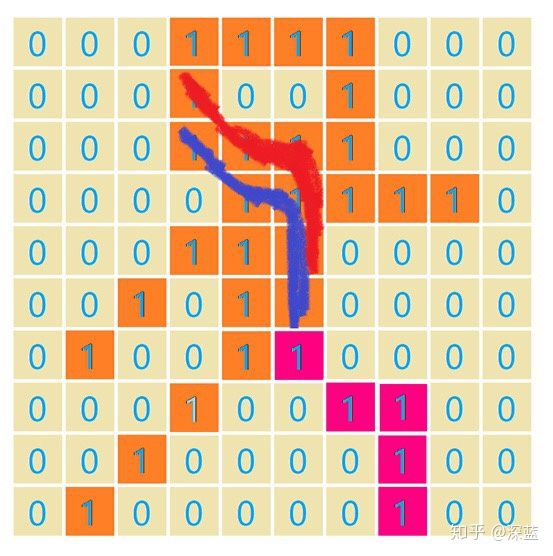
类似的:

分别取下面卷积核对第一层输出处理

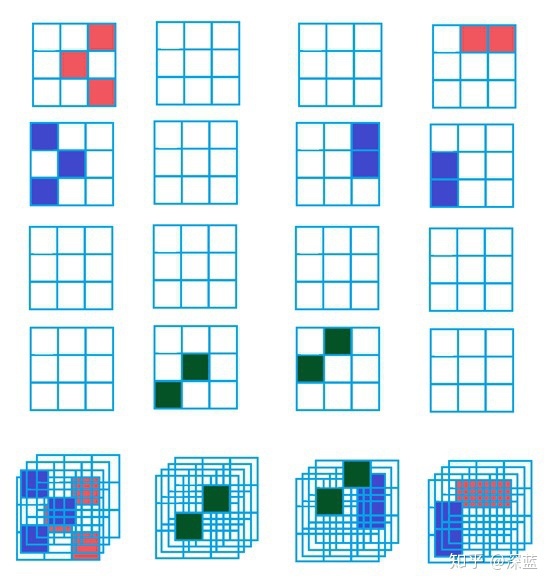
得到输出结果为：

顺便将它们三维化:

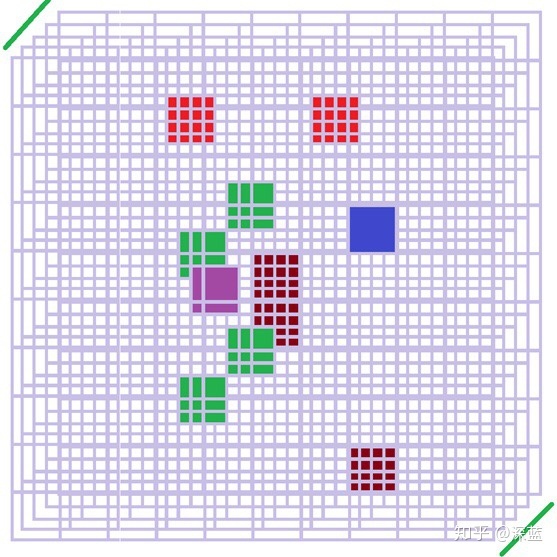
上图便是对“前腿”，“头”，“后腿”，“左臂”，“右臂”的检测结果（可以看出有些结构检测到不只一个；而对于头部，我们也是分为前后两部分分别检测的）。

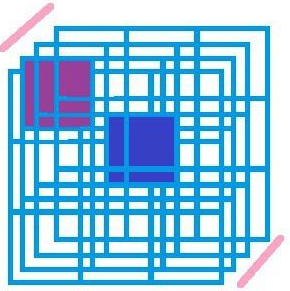
所以我们怎么利用上层输出，来预测要检测的“图片”中是否有人呢？这就需要全连接层了，这里不做过多讨论，不过对于本例子，我觉得全连接层可以理解为一把锁，而钥匙便是上层输出，当锁孔与钥匙匹配时，锁就能被打开。见下图：

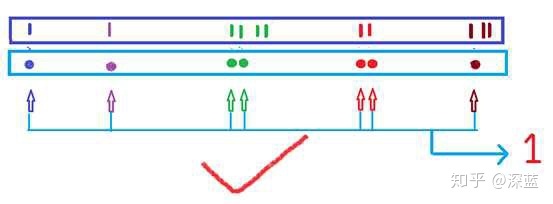
要进行最后一层的操做，我们需要将上层输出展开，也就是将三维结构的数据展为一维。图上紫色方框便是展开后的一维数据，也就是我所比喻的“锁”，而青色便是“钥匙”，当两者相匹配时输出为“1”；当然，如果不匹配的话，输出为“0”。

如图：

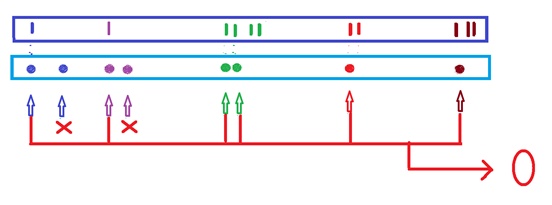
实际中的Fully Connect层要做的不止图上画的这些，权重也不能理解为简单的钥匙。就是说我们的这把“钥匙”不仅要考虑“凸”的地方，还要考虑“凹”的地方，因为全连接层还要对一些节点做出“惩罚”。打个比方就能明白，在本例子中，如果我们输入的图片对应的像素值全为“1”，相当于一张只有白色的图片，经过卷积也能提取很多信息，但最后结果肯定不应该输出为“1”，所以还要对一些节点做出“惩罚”，当“惩罚”太大时输出就不是“1”了。